Vector hash collision comparisons in Python

This short post is based on my repo of a similar name, all code can be found from there.

At the time of the original writing of this text I had been reading through Luciano Ramalho's excellent Fluent Python. In chapter nine, A Pythonic Object, we build a pythonic implementation of a 2-dimensional vector object, and in the next chapter extend it to an n-dimensional vector. At one point in the chapter we want to make the object hashable by implementing the __eq__ and __hash__ methods. The first iteration implements the hash of a vector by taking a XOR of each of the component hashes. This works, but since XOR is a commutative operator, what follows is that any two vectors whose components are permutations of each other, e.g. (1, 4, 9) and (9, 4, 1), will have the same hash.

Since the example is meant to be instructional, this is not a critical performance issue, but it did make me curious to see how the different hashes might affect the amount of hash collisions. A good way to measure hash collisions for a vector type, at least in my mind, was to create a list of 2000 vectors and and add them one by one into a set, measuring how long this takes. I thought that the results might interest other as well.

The full source code that I used is available in the repo (it started pretty, then turned more and more hackish, sry, for sure I'll come back to it one day and make it prettier¹), but for the basic idea is that we have the following two types of vectors, with the main idea copied from Fluent Python:

from array import array
import functools
import operator

class BaseVector:
    typecode = 'd'

    def __init__(self, iterable_input):
        self._components = array(self.typecode, iterable_input)

    def __iter__(self):
        return iter(self._components)

    def __eq__(self, other_vector):
        return tuple(self) == tuple(other_vector)

# The two actual vectors we use are as follows, both count both types of hashes
# for the vector, but return only one, to make the timing more consistent.

class SimpleVector(BaseVector):
    def __hash__(self):
        better_hash = hash(tuple(self._components))

        hash_collection = (hash(element) for element in self._components)
        simple_hash = functools.reduce(operator.xor, hash_collection, 0)

        return simple_hash

class BetterVector(BaseVector):
    def __hash__(self):
        better_hash = hash(tuple(self._components))

        hash_collection = (hash(element) for element in self._components)
        simple_hash = functools.reduce(operator.xor, hash_collection, 0)

        return better_hash

What we then do is that for each dimension $n$ going from 2 to 100, we generate four arrays of 2000 vectors, each of the following type:

• SimpleVector filled with n random integers 0-9.

• SimpleVector filled with n random floats from the unit interval [0,1].

• BetterVector filled with n random integers 0-9.

• BetterVector filled with n random floats from the unit interval [0,1].

For each of these four arrays we look how much it takes to add them all to a set one by one - as sets are implemented as hash tables, a large amount of hash collisions should correspond with longer filling time. Below we have plotted the results on 1) how increasing the dimension effects the set-filling times of each type of vector array and 2-4) what is the linear behaviour of the first three types of vectors. (The behaviour of BetterVector was identical when comparing integer or float filling, so we omitted the latter.)

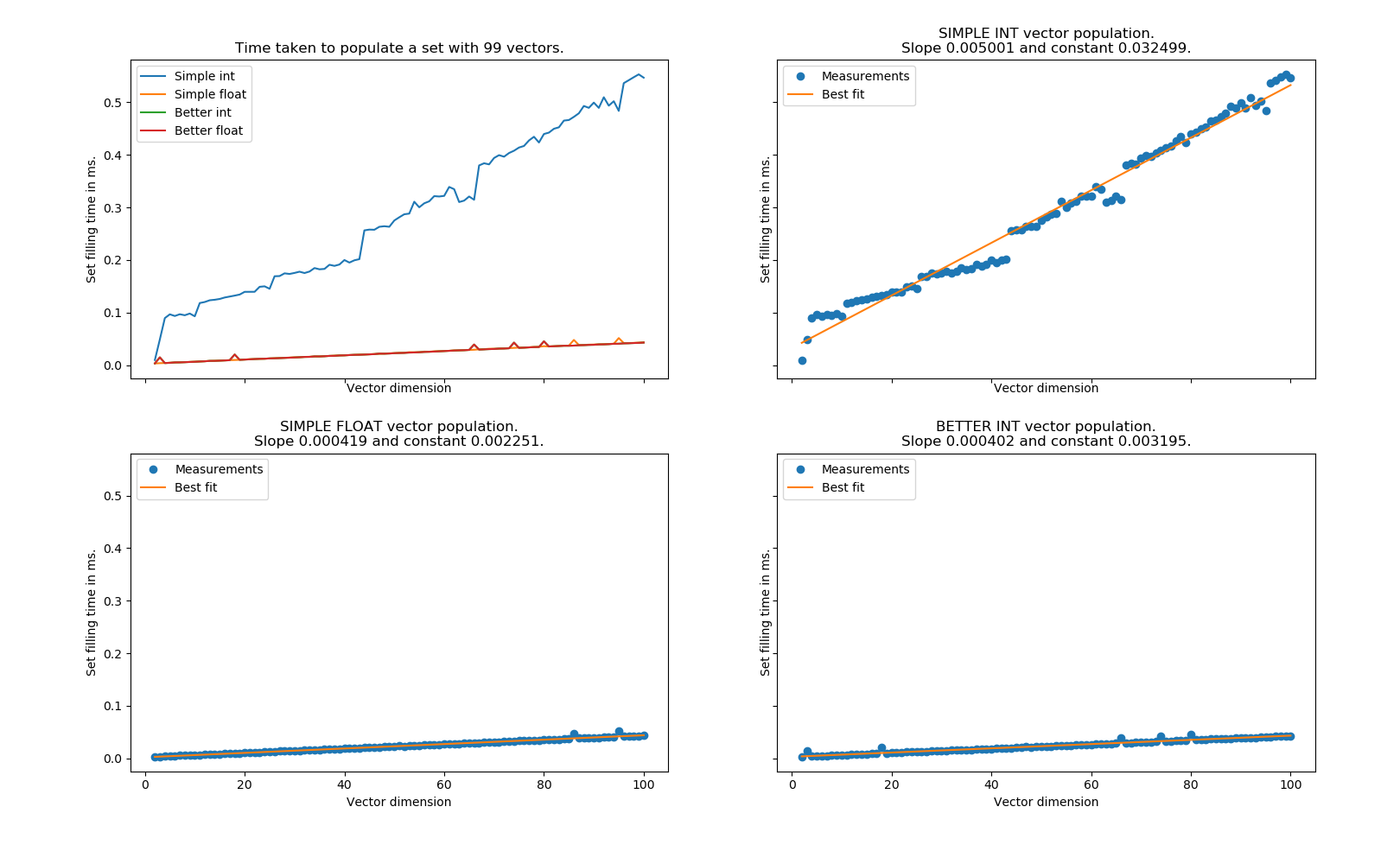
What is quite obvious from all of this is, that the longer a vector you have, the fewer ways you have to fill the slots with integers 0-9 without creating vectors that are permutations of each other, and thus you get more hash collisions with the simple hash. I can't quite be bothered to do the math, but is is interesting to note that the increase is roughly linear. Maybe one day I'll go through the combinatorics and see how well this corresponds to theoretical expectations². What is also interesting is that the line is not completely linear, and in a later picture you'll see that some of the jagged parts persist in other runs as well, so they are not completely random artifacts from the randomness of the process. My personal guess is that CPython is doing something clever in the background when deciding on what size of hash table it's gonna prepare for the job.

As can also be guessed, if we run the experiment again, but when filling with integers we allow them to vary from 0-200 instead of 0-9, the amount of hash collisions drastically reduces. (Note the chane

Furthermore, if we see what happens when the integer range is (0, N) where N is in [2, 10, 20, 200], we get the following comparison; in particular we see these clear dips around 42, 78 and maybe 95-ish that seem to persist even in very different kind data.

So, summa summarum, the set filling times seem to increase linearly with dimension regardless of the hash type you implement, but the slope can vary by orders of magnitude depending on the situation.