 Figure: DALL-E's rendition of a race between Python and C.
Figure: DALL-E's rendition of a race between Python and C.
This is mostly a mirror of my repo of the topic. The text has been written in a sort of diary format. The repo itself claims to be 'under construction' with more solver variations appearing in the future, but to be honest this is doubtful. For all the code see the repo; any filepath references should be taken relative to that.
Prologue - What are working with?
The goal here is to study the speed increases that I as a particular Python dev can achieve by going from 'naive Python' to using either more pythonic tools, using C-powered libraries like numpy, or by at the extreme using straight up C-code. This is less cutting-edge research and more of a personal learning diary. If you want to see a more serious study of the topic, see e.g. this.
Why?
C is faster than Python. There is very little question about that. But there is a much smaller difference between C and a Python program correctly using the C-based fast parts of Python or one of the fast C-based libraries like Numpy. In particular, in many cases (including mine) the important question is whether I the Python programmer could write C-code that runs faster than the implementations that rely on the Python libraries whose C backends have been written by professional C developers.
To choose a target for our speedup attempts, we're gonna look at a straightforward recursive Sudoku solver. To put all to the same page with the terminology, a sudoku is a logical game where you have a 9x9 grid divided into 9 3x3 blocks:
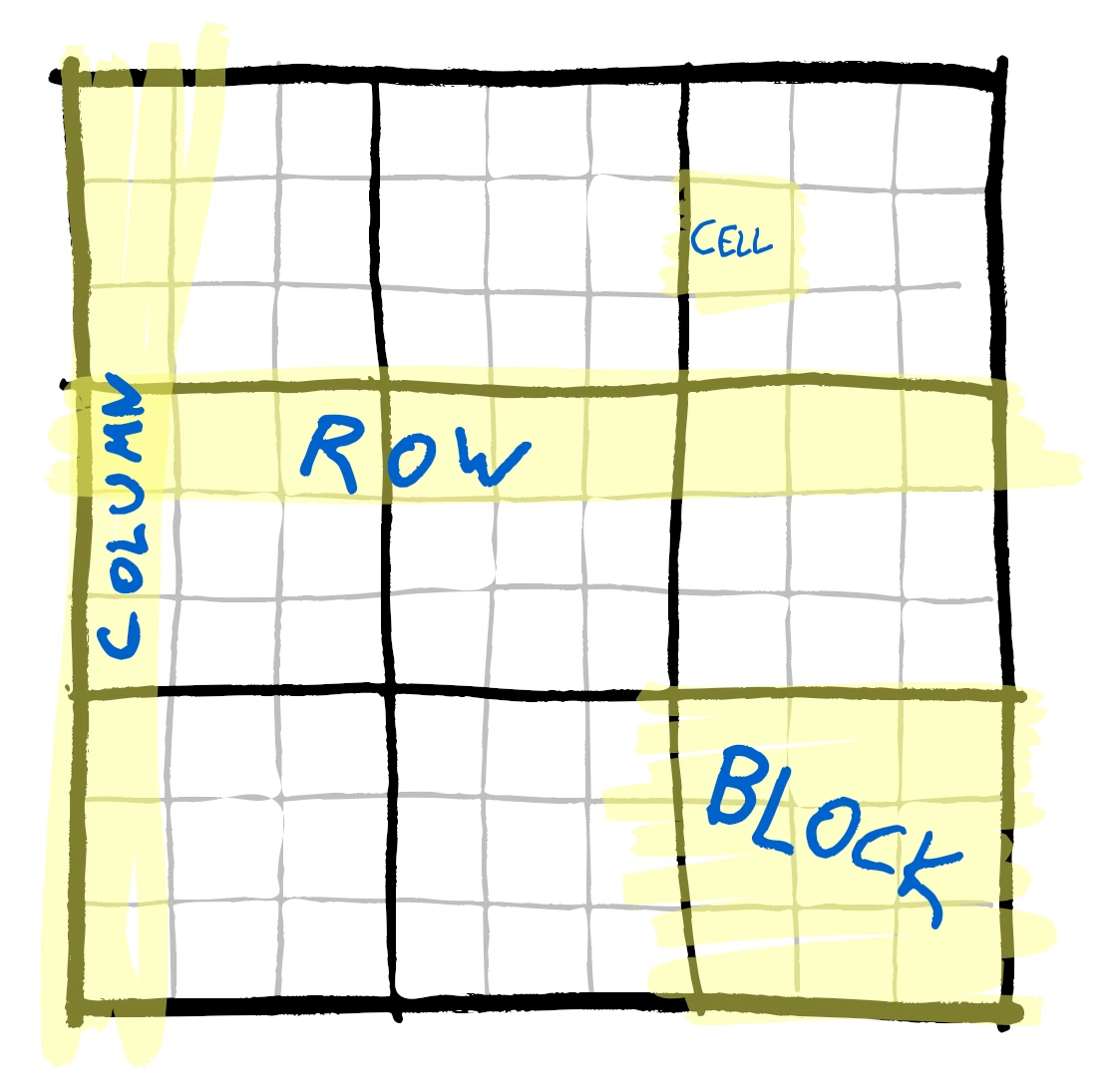
The rule of the game is to fill the grid with numbers 1-9 such that any row, column or block contains each of the numbers 1-9 exactly once. The difficulty of the game depends on which cells have been pre-filled with which numbers. Estimating the difficulty of a sudoku is a non-trivial task, though if you are given starting configuration that has only one solution then adding legal numbers always makes it easier. (Removing them might not since multiple solutions might emerge by reducing restrictions, and if the starting solution has multiple solutions then adding a number might rule out simpler solutions.)
For the system we'll handle data input and output as strings of numbers, i.e. a single sudoku will be an string of length 81, with each character one of the numbers 0-9. Here with a 0 we will mean that a cell is unfilled. The numbers in this string are taken to be in such an order that they fill the standard 9x9 grid one by one, starting from top left and moving through the cells left to right, top to bottom.
Internally we'll handle the Sudoku as a 9x9 grid of possibilities. By this I mean that the content of any given sudoku cell will be an array of booleans, where each index is representing if a given number could be allowed in that cell. We do this instead of just having a 9x9 grid of numbers 0-9 for two reasons: - This base architecture makes it much easier to include some more complicated strategies. - We don't want to make the algorithm and the underlying structure too simple. Benchmarking Python vs Numpy vs C with a for loop doesn't sound interesting enough.
So the basic structure we'll look at will be something we call a possibility grid:
boolean p_grid[NUM_ROWS][NUM_COLS][NUM_POSSIBILITIES]
though all of the LITERAL_CONSTANTS here are actually just 9 and, depending on the
version of the solver, instead of booleans we might be using integers or chars.
Anyway, pseudocode for the main solver will look like this:
def recursive_solver(sudoku : PossibilityGrid) -> bool: changed = True while(changed): changed = reduce_possibilities(sudoku) # Clever strategies if is_solved(sudoku): return True # Recursive brute forcing starts here: cell_idx = first_unsolved_cell_index(sudoku) possibilities = get_cell_possibilities(cell_idx, sudoku) for p in possibilities: local_sudoku = sudoku.copy() set_cell_of_sudoku(cell_idx, local_sudoku, p) result = recursive_solver(local_sudoku) if result: return True return False
So here the reduce_possibilities is responsible for clever strategies like "for this cell, the only number not yet appearing in its row, col and block is 5, so the only possibility for this cell is 5". The latter recursive part will just start brute forcing the solution after the clever stuff has failed.
What's our benchmark data?
I found a nice open source (Public Domain licennse)
sudoku source on (kaggle)[https://www.kaggle.com/datasets/rohanrao/sudoku].
From that I sampled randomly 10k sudokus, which can be found in the folder ./data/ as a csv. This turned out to be a big enough sample to get various levels of difficulty without being too slow to wait to complete.
Chapter 1 - Python versus C in various rounds
The main idea is that I take turns improving my Python solvers and C solvers, with the aim of alternatively trying to close the gap with the Python versions and then trying to expand the gap with C versions. The benchmarks were run (at the time of writing) on an Azure VM B2ms (2 vcpus, 8 GiB memory) running Ubuntu 18.04. In my rudimentary scorecard, getting Python within an order of magnitude range of C is a draw, and getting Python to take less than 5x the time that C takes is a win for Python.
Round 1 - The baseline - Simple Python vs Simple C
For the first iteration I built a very straightforward implementation in Python
./src/naive_sudoku_solver.py.
It's called naive because it doesn't do anything fancy, though it aims to be as pythonic as possible
and not do too much obviously stupid things. On the benchmark machine it solved
10k sudokus in just under 50 seconds.
To compete the naive Python version, I then made a simple C-version ./C-version/sudoku_solver.c.
I call it simple because simple C is the best I can do, and it probably does some obviously stupid things as well because I don't
have a good touch to C. But in any case it not only compiles but also runs and using the same algorithm it solves the same 10k
sudokus correctly in about 5 seconds - so an order of magnitude improvement right off the bat.
| s/Sudoku | 10k Sudokus | |
|---|---|---|
| Naive Python | 5.1e-03 | 51s |
| Naive C | 5.4e-04 | 5.2s |
So as expected, C is much much faster but with our scoring system we're "only" an order of magnitude apart so we're calling this a draw. Let's see how we could start improving the Python version a bit.
Round 1.5 - OOP solution
Before we start to do anything fancy, I see that we're gonna be building Sudoku solvers that improve or extend previous versions. Shouldn't we maybe do this in a more Object Oriented Programming way? It should surely make this nice in the long run, but doesn't OOP create extra baggage that will slow everything down? Let's test this!
So in ./src/OOP_sudoku.py we have the very same solver as before, but in as a Sudoku Solving Object. We run the results again and what we see is:
| s/Sudoku | 10k Sudokus | |
|---|---|---|
| Naive Python | 5.1e-03 | 51s |
| Naive C | 5.4e-04 | 5.2s |
| OOP Python | 4.9e-03 | 49s |
So no, the Object structure doesn't bring any extra baggage, we're even a bit faster than we were with the naive solution. If we find1 the energy, we'll later on try to understand why we were faster here. (I wouldn't be surprised if the answer has something to do with "optimizing bytecode interpreter".)
Round 2 - Improved Naive Python
Let's start small before even trying to bring out the big guns. We take the OOP solver and try and see if there is anything to optimize along the lines of "iterating over (long) lists is slow, dicts and other hash-table based things are fast".
Analysis
First of all let's look at where we actually spend time in our current OOP solver by running the benchmark for that solver under cProfile:
python -m cProfile -o OOP_solver.prof benchmark.py
The results are kinda long, but let's look at the top time spenders based both on cumulative time which counts even when the given function has called another function (and waiting for its results) and on total time which excludes time in sub-functions. The commands we run look like this:
$ python -m pstats OOP_solver.prof
Welcome to the profile statistics browser.
OOP_solver.prof% strip
OOP_solver.prof% sort cumtime
OOP_solver.prof% stats 30
[...]
OOP_solver.prof% sort tottime
OOP_solver.prof% stats 30
And here are the results, first for cumulative time:
Mon Mar 6 10:11:01 2023 OOP_solver.prof
252249901 function calls (252235248 primitive calls) in 114.974 seconds
Ordered by: cumulative time
List reduced from 696 to 30 due to restriction <30>
ncalls tottime percall cumtime percall filename:lineno(function)
44/1 0.000 0.000 115.336 115.336 {built-in method builtins.exec}
1 0.000 0.000 115.336 115.336 benchmark.py:1(<module>)
1 0.066 0.066 115.315 115.315 benchmark.py:15(run_benchmark)
10000 0.038 0.000 114.444 0.011 OOP_sudoku.py:4(read_and_solve_sudoku_from_string)
24019/10000 0.170 0.000 112.645 0.011 OOP_sudoku.py:80(recursive_solver)
84712 9.148 0.000 78.545 0.001 OOP_sudoku.py:171(reduce_possibilities)
2135653 6.198 0.000 66.217 0.000 OOP_sudoku.py:197(get_simple_mask)
6406959 21.542 0.000 44.162 0.000 OOP_sudoku.py:54(extract_exclusions)
84712 1.542 0.000 29.708 0.000 OOP_sudoku.py:137(still_solvable)
2287224 11.333 0.000 19.849 0.000 OOP_sudoku.py:44(collision_in_collection)
88109228 17.485 0.000 17.639 0.000 {built-in method builtins.sum}
2898061 9.392 0.000 11.871 0.000 OOP_sudoku.py:113(block)
46275920 6.938 0.000 6.938 0.000 {method 'index' of 'list' objects}
62948777 6.190 0.000 6.190 0.000 {method 'append' of 'list' objects}
6406959 5.310 0.000 5.310 0.000 OOP_sudoku.py:56(<listcomp>)
2898061 1.881 0.000 4.605 0.000 OOP_sudoku.py:110(col)
84712 0.745 0.000 3.981 0.000 {built-in method builtins.all}
6664729 1.971 0.000 3.238 0.000 OOP_sudoku.py:156(<genexpr>)
2135653 3.202 0.000 3.202 0.000 OOP_sudoku.py:210(<listcomp>)
6406959 2.807 0.000 2.807 0.000 OOP_sudoku.py:62(<listcomp>)
24019 1.178 0.000 2.748 0.000 OOP_sudoku.py:241(__str__)
2898061 2.724 0.000 2.724 0.000 OOP_sudoku.py:111(<listcomp>)
14019 0.031 0.000 2.444 0.000 OOP_sudoku.py:231(copy)
2824460 1.079 0.000 1.987 0.000 OOP_sudoku.py:19(p_array_to_num)
24019 0.024 0.000 1.425 0.000 OOP_sudoku.py:76(__init__)
24019 0.732 0.000 1.401 0.000 OOP_sudoku.py:28(convert_sudoku_string_to_p_grid)
16974 0.292 0.000 0.937 0.000 OOP_sudoku.py:127(first_unsolved_cell_index)
4295 0.814 0.000 0.814 0.000 OOP_sudoku.py:234(import_p_grid)
10001 0.018 0.000 0.771 0.000 std.py:1174(__iter__)
795 0.015 0.000 0.750 0.001 std.py:1212(update)
and then for total time:
Mon Mar 6 10:11:01 2023 OOP_solver.prof
252249901 function calls (252235248 primitive calls) in 114.974 seconds
Ordered by: internal time
List reduced from 696 to 30 due to restriction <30>
ncalls tottime percall cumtime percall filename:lineno(function)
6406959 21.542 0.000 44.162 0.000 OOP_sudoku.py:54(extract_exclusions)
88109228 17.485 0.000 17.639 0.000 {built-in method builtins.sum}
2287224 11.333 0.000 19.849 0.000 OOP_sudoku.py:44(collision_in_collection)
2898061 9.392 0.000 11.871 0.000 OOP_sudoku.py:113(block)
84712 9.148 0.000 78.545 0.001 OOP_sudoku.py:171(reduce_possibilities)
46275920 6.938 0.000 6.938 0.000 {method 'index' of 'list' objects}
2135653 6.198 0.000 66.217 0.000 OOP_sudoku.py:197(get_simple_mask)
62948777 6.190 0.000 6.190 0.000 {method 'append' of 'list' objects}
6406959 5.310 0.000 5.310 0.000 OOP_sudoku.py:56(<listcomp>)
2135653 3.202 0.000 3.202 0.000 OOP_sudoku.py:210(<listcomp>)
6406959 2.807 0.000 2.807 0.000 OOP_sudoku.py:62(<listcomp>)
2898061 2.724 0.000 2.724 0.000 OOP_sudoku.py:111(<listcomp>)
6664729 1.971 0.000 3.238 0.000 OOP_sudoku.py:156(<genexpr>)
2898061 1.881 0.000 4.605 0.000 OOP_sudoku.py:110(col)
84712 1.542 0.000 29.708 0.000 OOP_sudoku.py:137(still_solvable)
24019 1.178 0.000 2.748 0.000 OOP_sudoku.py:241(__str__)
2824460 1.079 0.000 1.987 0.000 OOP_sudoku.py:19(p_array_to_num)
4295 0.814 0.000 0.814 0.000 OOP_sudoku.py:234(import_p_grid)
84712 0.745 0.000 3.981 0.000 {built-in method builtins.all}
24019 0.732 0.000 1.401 0.000 OOP_sudoku.py:28(convert_sudoku_string_to_p_grid)
2898061 0.513 0.000 0.513 0.000 OOP_sudoku.py:107(row)
4577538/4577451 0.494 0.000 0.494 0.000 {built-in method builtins.len}
799 0.373 0.000 0.373 0.000 {method 'write' of '_io.TextIOWrapper' objects}
16974 0.292 0.000 0.937 0.000 OOP_sudoku.py:127(first_unsolved_cell_index)
1945539 0.200 0.000 0.200 0.000 {method 'copy' of 'list' objects}
24019/10000 0.170 0.000 112.645 0.011 OOP_sudoku.py:80(recursive_solver)
464825 0.110 0.000 0.153 0.000 utils.py:330(<genexpr>)
24019 0.108 0.000 0.670 0.000 OOP_sudoku.py:31(<listcomp>)
1 0.066 0.066 115.315 115.315 benchmark.py:15(run_benchmark)
462434 0.044 0.000 0.044 0.000 {built-in method unicodedata.east_asian_width}
For now I think the best place to focus on is the top of the total time, in particular these lines:
ncalls tottime percall cumtime percall filename:lineno(function)
6406959 21.542 0.000 44.162 0.000 OOP_sudoku.py:54(extract_exclusions)
88109228 17.485 0.000 17.639 0.000 {built-in method builtins.sum}
2287224 11.333 0.000 19.849 0.000 OOP_sudoku.py:44(collision_in_collection)
2898061 9.392 0.000 11.871 0.000 OOP_sudoku.py:113(block)
84712 9.148 0.000 78.545 0.001 OOP_sudoku.py:171(reduce_possibilities)
46275920 6.938 0.000 6.938 0.000 {method 'index' of 'list' objects}
2135653 6.198 0.000 66.217 0.000 OOP_sudoku.py:197(get_simple_mask)
62948777 6.190 0.000 6.190 0.000 {method 'append' of 'list' objects}
So here we see that the biggest time consumers consist of a few built-in methods -
sum, list.index and append - together with a few methods we've built, namely
extract_exclusions, collisions_in_collection, block, reduce_possibilities and get_simple_mask.
Looking at how these transgressors interact, we note that the appending to list only happens
in the methods collisions_in_collection, block, reduce_possibilities and the magic
method __str__ which is used in the copying of a sudoku.
The built-in sum method is also used only in methods listed above, together with another
static method called p_array_to_num which has also found its way to the top 30 of both lists.
So looking how these different subparts consume our CPU time, we note that there might be chances to improve. For example, looking at our extract_exclusions method which holds top rank in both total and cumulative times, we see that we are using the sum only to detect if a given
possibility array is already completely determined. And in fact, most of the uses of sum
are only used to figure out if a given possibility array has only a single '1' in it. This seeems
like an overkill.
So instead of sums, let's do a faster lookup. There are only 9 possibilities for an array of length 9 to have only one '1', so let's enumerate them and turn the check into a dictionary lookup. To do this, though, we need something hashable, so we need to turn from lists to tuples. Let's go one step further: we'll change the whole Sudoku data format from 3-dimensional list to a 2-dimensional list of tuples!
So what we changed going from OOP_sudoku.py to OOP_sudoku_improved.py was:
1. Turned the whole "from possibility array to number and back" thing to rely on
dictionary lookups of pre-stored tuples.
2. Changed the internal sudoku format to have all the possibility arrays to be tuples
instead of lists.
3. Reduced for loops by adding more early returns, plus other minor improvements.
And here are the results:
| s/Sudoku | 10k Sudokus | |
|---|---|---|
| Naive Python | 5.1e-03 | 51s |
| Naive C | 5.4e-04 | 5.2s |
| OOP Python | 4.9e-03 | 49s |
| Improved OOP Python | 4.7e-03 | 47s |
So with all that work we shaved about four percents off our running time. cProfiler tells that for the total time the biggest time users are now:
ncalls tottime percall cumtime percall filename:lineno(function)
6406959 20.422 0.000 33.407 0.000 OOP_sudoku_improved.py:47(extract_exclusions)
81526820 16.343 0.000 16.343 0.000 OOP_sudoku_improved.py:35(p_array_to_num)
2287224 9.319 0.000 15.190 0.000 OOP_sudoku_improved.py:73(collision_in_collection)
84712 9.137 0.000 65.780 0.001 OOP_sudoku_improved.py:179(reduce_possibilities)
2898061 8.713 0.000 10.813 0.000 OOP_sudoku_improved.py:124(block)
2135653 5.703 0.000 53.776 0.000 OOP_sudoku_improved.py:205(get_simple_mask)
62948777 5.046 0.000 5.046 0.000 {method 'append' of 'list' objects}
2135653 3.099 0.000 3.099 0.000 OOP_sudoku_improved.py:218(<listcomp>)
6406959 2.731 0.000 2.731 0.000 OOP_sudoku_improved.py:49(<listcomp>)
2898061 2.562 0.000 2.562 0.000 OOP_sudoku_improved.py:122(<listcomp>)
2898061 1.776 0.000 4.338 0.000 OOP_sudoku_improved.py:121(col)
So one of the big differences is that we pushed the 17 or so seconds used by sum to the
p_array_to_num function here. So I guess the lesson here is that sum(short_list) == 1 is also very fast as it is on par with essentially hash-table lookups? We might even conjecture that Python's built-in functions might be quite heavily optimized.
Round 3 - Numpy
So, our first speedup attempts had modest results. Maybe we've used up all the easy tricks in relying on fast parts of standard Python? Let's try and see if we can do more by using the fast Python library, i.e. Numpy.
The logic behind this approach is that Sudoku is pretty much a glorified matrix, and numpy is good with matrices.
This should be a no-brainer. In ./src/numpy_sudoku.py we have the OOP solver rewritten in such
a way that the sudoku is not a 3-dimensional list but a 3-dimensional numpy-integer array.
| s/Sudoku | 10k Sudokus | |
|---|---|---|
| Naive Python | 5.1e-03 | 51s |
| Naive C | 5.4e-04 | 5.2s |
| OOP Python | 4.9e-03 | 49s |
| Improved OOP Python | 4.7e-03 | 47s |
| First numpy solver | 3.3e-02 | 330s |
So the first attempt to numpy solve this is that we spend an order of magnitude more solving it. This is pretty much the opposite of what I wanted. Let's fire up the good old cProfile to see what is going on.
From numpy_solver.prof we get again:
Tue Mar 7 11:28:23 2023 numpy_solver.prof
456300559 function calls (456284372 primitive calls) in 515.038 seconds
Ordered by: internal time
List reduced from 1230 to 20 due to restriction <20>
ncalls tottime percall cumtime percall filename:lineno(function)
28669199 65.544 0.000 65.544 0.000 {method 'reduce' of 'numpy.ufunc' objects}
84712 53.859 0.001 395.698 0.005 numpy_sudoku.py:159(reduce_possibilities)
6406959 52.711 0.000 67.175 0.000 function_base.py:5054(delete)
8694183 38.006 0.000 217.958 0.000 numpy_sudoku.py:60(get_fixed_projection_array)
50766043 36.277 0.000 240.813 0.000 {built-in method numpy.core._multiarray_umath.implement_array_function}
19861988 26.811 0.000 87.349 0.000 fromnumeric.py:69(_wrapreduction)
8807211 22.568 0.000 56.763 0.000 numpy_sudoku.py:20(p_array_to_num)
17490052 20.292 0.000 102.563 0.000 fromnumeric.py:2188(sum)
2898061 17.290 0.000 23.512 0.000 numpy_sudoku.py:110(block)
17490052 13.594 0.000 128.313 0.000 <__array_function__ internals>:177(sum)
6406959 10.396 0.000 252.591 0.000 numpy_sudoku.py:53(extract_exclusions)
2135653 10.322 0.000 10.322 0.000 numpy_sudoku.py:198(<listcomp>)
8694183 10.192 0.000 10.192 0.000 {method 'take' of 'numpy.ndarray' objects}
Tue Mar 7 11:28:23 2023 numpy_solver.prof
456300559 function calls (456284372 primitive calls) in 515.038 seconds
Ordered by: cumulative time
List reduced from 1230 to 30 due to restriction <30>
ncalls tottime percall cumtime percall filename:lineno(function)
141/1 0.000 0.000 515.038 515.038 {built-in method builtins.exec}
1 0.000 0.000 515.038 515.038 benchmark.py:1(<module>)
1 0.048 0.048 514.884 514.884 benchmark.py:20(run_benchmark)
10000 0.048 0.000 513.466 0.051 numpy_sudoku.py:5(read_and_solve_sudoku_from_string)
24019/10000 0.216 0.000 500.796 0.050 numpy_sudoku.py:77(recursive_solver)
84712 53.859 0.001 395.698 0.005 numpy_sudoku.py:159(reduce_possibilities)
2135653 10.143 0.000 294.213 0.000 numpy_sudoku.py:185(get_simple_mask)
6406959 10.396 0.000 252.591 0.000 numpy_sudoku.py:53(extract_exclusions)
50766043 36.277 0.000 240.813 0.000 {built-in method numpy.core._multiarray_umath.implement_array_function}
8694183 38.006 0.000 217.958 0.000 numpy_sudoku.py:60(get_fixed_projection_array)
17490052 13.594 0.000 128.313 0.000 <__array_function__ internals>:177(sum)
17490052 20.292 0.000 102.563 0.000 fromnumeric.py:2188(sum)
19861988 26.811 0.000 87.349 0.000 fromnumeric.py:69(_wrapreduction)
84712 2.751 0.000 86.997 0.001 numpy_sudoku.py:124(still_solvable)
6406959 5.251 0.000 78.532 0.000 <__array_function__ internals>:177(delete)
2287224 6.429 0.000 75.701 0.000 numpy_sudoku.py:47(collision_in_collection)
6406959 52.711 0.000 67.175 0.000 function_base.py:5054(delete)
28669199 65.544 0.000 65.544 0.000 {method 'reduce' of 'numpy.ufunc' objects}
8807211 22.568 0.000 56.763 0.000 numpy_sudoku.py:20(p_array_to_num)
8694183 6.475 0.000 36.872 0.000 <__array_function__ internals>:177(take)
14855826 9.852 0.000 25.918 0.000 <__array_function__ internals>:177(where)
We see especially from the total time calculations that we are spending a lot of time doing numpy-internal methods like reduce, delete and implement_array_function. My very non-expert feeling here is that we are paying a lot for the overhead of the numpy machinery that allows us to make really fast computations for large dimensional linear algebra calculations? Also Numpy tends to excel for computations that can be vectorized, and here we are doing a lot of for loops instead.
So my current guess2 is that not using numpy for vectorized calculations is killing our speed improvements and numpy overhead is pushing us to the red.
Sidenote - Using profiling to test for recursion paths
Note that in this line:
ncalls tottime percall cumtime percall filename:lineno(function)
24019/10000 0.216 0.000 500.796 0.050 numpy_sudoku.py:77(recursive_solver)
we can easily see from ncalls that the main recursive solver was called 10k times at the outset,
and then 24k times internally. This gives not only an average recursion depth, but seeing that this
number is the same for all the different versions of Python sudoku solvers we've used, we have strong
evidence that they are using essentially the same recursive algorithm with same recursion depths.
So the problem with the numpy version shouldn't be some subtle mistake about the recursive part not exiting early enough, but just about the numpy version not being faster.
Interlude - What did we learn here?
Premature optimization is the root of all evil.
So, before actually trying to do this, my knee-jerk reaction would have been to do this with numpy since numpy is fast with matrices. Turns out that that would have been a bad idea. Especially if I hadn't had a resonable naive version as a base case comparison.
In hindsight maybe the library that is built to handle 1 000 000 -dimensional float arrays and matrix multiplications of similar dimensions has some overhead when used to handle a 9x9x9 matrix of ones and zeroes? Who knew! (Option two: I'm doing something stupid with numpy here. At some point I'll go find3 numpy-based sudoku solvers of other people and see how they did it - probably the idea is to pivot your viewpoint to something less human-approach -centric.)
Chapter 2 - Using C within Python
If you can't beat them, join them! Next we'll try and see how to use the superiorly fast C in Python versions. Our benchmarking script already has two ways of invoking the C-code, both in the badly named ./src/CLI_C_caller.py file and both using the os.popen to run a bash command that invokes the compiled executable of the naive C-version.
The one we've used so far passes the test data csv filepath as a parameter:
def run_C_benchmark(test_data_filepath) -> str: stream = os.popen(f'./C-version/a.out -B "{test_data_filepath}"') output = stream.read() return output
Here the C-code is responsible for reading the file contents.
Another way would be to pass not the filepath to read but the Sudoku to solve as a string:
def read_and_solve_sudoku_from_string(input_sudoku: str) -> str: stream = os.popen(f"./C-version/a.out -r {input_sudoku} -S") output = stream.read() return output.strip("\n")
This relies on Python to read the file and then passes the Sudokus to the C-part one by one.
Let's see how much time we lose in piping the data from Python to C through the command line one-by-one:
| s/Sudoku | 10k Sudokus | |
|---|---|---|
| Naive Python | 5.1e-03 | 51s |
| C - CSV | 5.4e-04 | 5.7s |
| C - line-by-line | 2.4e-03 | 49s |
This seems to imply that the overhead of piping the data through popen/bash is quite large. So the the natural step feels to be to transform the C-system into something we can call from Python directly!
After studying the Real Python tutorial on the topic, it was almost easy4 to turn my C-code into a Python package. It's not great C nor great Python, but it works and that's what matters for now.
Anyway. ./C-version/sudoku_solver_module.c contains the module that can be turned into a Python package called RamiSudoku. To do this, after activating your virtual environment,
run python setup.py install in the folder ./C-version.
How's the speed now then?
| s/Sudoku | 10k Sudokus | |
|---|---|---|
| Naive Python | 5.3e-03 | 53s |
| C - CSV | 5.7e-04 | 5.7s |
| C - line-by-line | 2.4e-03 | 24s |
| C based Python package | 1.1e-04 | 1.1s |
So, somewhat surprisingly, the Python-packaged version is five times faster than my naive C. I'm guessing here that the Python file reader was written by an actually competent C-developer, unlike my version of getting the test and comparison data from the csv. I do not currently have the energy to learn how to profile my C-code to verify if this really is the case.
Python 3.11
Speaking of competent developers, the word on the street is that Python 3.11 can provide considerable speed improvements compared to earlier versions. If I recall correctly, one of the main improvements has to do with more clever handling of data structures. This sounds like something that could benefit our algorithms since our main objects are really just lists/tuples of a specific type, not of generic objects. Let's run the benchmarks again but compare to Python 3.11 when suitable!
| 10k Sudokus w/ 3.10 | 10k Sudokus w/ 3.11 | Speed increase | |
|---|---|---|---|
| Naive Python | 53s | 42s | 23% |
| OOP Python | 50s | 40s | 25% |
| Improved OOP Python | 48s | 37s | 30% |
| First numpy solver | 350s | 320s | 9% |
| C - CSV | 5.7s | 5.4s | 5% |
| C - line-by-line | 24s | 24s | 0% |
| C based Python package | 1.1s | 1.1s | 0% |
Not bad, 25-ish percent improvements on the more Python-heavy solutions, and even a 5% improvement on the wrapped C-benchmark.
Epilogue
What did we learn?
We learned a few things:
-
C is faster than Python when in the hands of a competent dev. My Python-packaged C-solver is faster than my raw C-solver, which clearly indicates that I am doing something silly in my C-version.
-
Read tutorials through and don't start to solo around. But if you don't and do, then when running to weird error messages, try to go back to patiently following the tutorial.
-
Don't (only) guess, always try out and test. I would not have guessed Numpy-version to be so slow or the C-extension module to be faster than my naive C-version.
What could be done better?
First of all, the algorithm is begging for improvements. E.g. the relatively minor change where the brute-force solver does not look for the first unsolved cell but the cell with least possibilities gives an immediate speedup by reducing the recursion count. A better approach would be to try and add some more clever reduction rules to the solver, and better yet would be to stop trying to solve this as a human would and use something much more cool.
-
We didn't. ↩
-
My first guess was that the numpy version would be much faster, so observing almost an order of magnitude slowdown we can deduce that my guesses on numpy are not to be trusted. ↩
-
Sure I will. ↩
-
As a caveat to those trying to repeat this: you're not supposed to compile
gcc sudoku_solver_module.c, it won't work and you'll spend hours trying to troubleshoot a wrong thing. ↩